이번 포스트에서는 탐색에 최적화된 이진탐색트리의 개념과 성질, 그리고 코드 구현 방법까지 알아보려 한다.
▣ 이진탐색트리 Binary Search Tree (BS 트리)
- 트리에서 특정 데이터의 효과적인 검색을 위해 제한점을 가지는 이진트리 형식의 자료구조다.
- 특정 데이터 검색, 노드 삽입, 삭제에 가장 효과적인 이진트리다.
- 탐색에 최적화된 이진트리다.
- key: 이진 트리에서 노드의 데이터
● 규칙
- 왼쪽 서브트리에 있는 모든 노드의 key값은 내 key값보다 작다.
- 오른쪽 서브트리에 있는 모든 노드의 key값은 내 key값보다 크다.

● 특성
- 같은 순서 데이터로 BS 트리를 여러가지 만들 수 있다.
- 루트 노드를 뭐로 잡느냐에 따라 다양하게 구성된다.

● 노드
struct KNode{
struct KNode *left; // 왼쪽 자식 가리키는 포인터 (항상 작음)
char key[10]; // key값
int info; // 데이터
struct KNode *right; // 오른쪽 자식 가리키는 포인터 (항상 큼)
}
● BS 트리 중위 순회중위순회 : 왼쪽자식 (Left) -> 부모출력 (Print) -> 오른쪽자식 (Right)
void Inorder(struct KNode *rootptr){
if(rootptr != null){
Inorder(rootptr->left);
cout << rootptr->info;
Inorder(rootptr->right);
}
}
● BS 트리에서 key값이 k인 노드 찾기
- if 트리가 빈 경우 -> 실패, else k와 현재 루트 노드의 key값 ki 비교.
- k == ki 면 탐색 성공! 노드는 Vi
- k < ki 면 Vi의 왼쪽 서브트리 탐색. Vi = Vi_left로 변경 후 1번 과정으로 이동.
- k > ki 면 Vi의 오른쪽 서브트리 탐색. Vi = Vi_right로 변경 후 1번 과정으로 이동.
struct KNode *Search(char k[], struct KNode *r){
if(r==null)
return(null);
else
if(strcmp(k, r->key) == 0) // 루트노드의 key값이 k일 때
return(r);
else if(strcmp(k, r->key) < 0) // k < 루트노드의 key값일 때
return Search(k, r->left);
else return Search(k, r->right); // k > 루트노드의 key값일 때
}
● BS 트리에 key값이 k인 노드 삽입
- if 트리가 빈 경우 -> key값이 k인 노드 삽입!! 끝, else k와 현재 루트 노드의 key값 ki 비교.
- k == ki 면 중단!!
- k < ki 면 Vi의 왼쪽 서브트리에 삽입. Vi = Vi->left로 변경 후 1번 과정으로 이동.
- k > ki 면 Vi의 오른쪽 서브트리에 삽입. Vi = Vi->right로 변경 후 1번 과정으로 이동.
struct KNode *Insert(struct KNode *newptr, struct KNode *r){
if(r == null)
return newptr;
else
if(strcmp(newptr->key, r->key) == 0)
DUPLICATE_ENTRY();
else
if(strcmp(newptr->key, r->key) < 0)
r->left = Insert(newptr, r->left)
else
r->right = Insert(newptr, r->right);
return r;
}
● BS 트리에서 key값이 k인 노드 삭제 ▶ 자식노드 1개만 갖는 노드 삭제 --> 삭제한 노드를 가리켰던 포인터가 삭제한 노드의 서브트리 루트를 가리키게 만든다. ▶ 자식노드를 2개 가지는 노드 삭제 --> 오른쪽 자식노드를 삭제노드 위치로 이동시킨다. 단, 오른쪽 자식노드가 없으면 왼쪽 자식노드를 위로 올린다.
● BS 트리 - SPLAY 트리 - BB 트리 - AVL 트리?
BS 트리에서 변형된 트리로 Splay트리, BB트리, AVL트리가 있다. 이 중 BB트리와 AVL트리는 균형트리라고 부른다.
▶ SPLAY 트리
- BS트리에서 탐색속도를 높이기 위해 고안된 트리
- 예전에 탐색했던 노드를 루트노드 쪽으로 올려서 더 빠르게 찾게 한다.
▶ BB 트리, AVL 트리
- BS트리에서 트리의 좌우 균형을 맞추도록 트리의 구조를 변형하여, 탐색 효율을 높이고자 고안된 트리 형식
SPLAY 트리가 나오게 된 자세한 배경을 알아보고 SPLAY 트리에 대해서도 알아보자.
▣ SPLAY 트리
SPLAY 트리는 자주 탐색하는 key를 가진 노드를 루트에 가깝게 위치하도록 한 BS 트리다. 그래서 비교 연산의 수를 줄여서 탐색 성능을 높인 트리 구조다.
● 이진 탐색 트리(BS 트리)의 한계
- BS 트리의 성능은 1) 트리의 구조와 2) 특정 노드에 접근할 확률에 영향받는다.
- 1) 때문에 특정 노드를 탐색, 삽입, 삭제할 때 최적의 BS 트리구조 결정이 어렵다.
- Heuristic 알고리즘을 사용하여 BS 트리를 만들었을 때 최적의 성능을 낸다.
● Heuristic 알고리즘?
- 자주 탐색하는 key를 가진 노드를 트리의 루트에 가까이 위치시킨다.
- 트리의 균형이 유지되도록 각 노드의 왼쪽, 오른쪽 서브트리가 비슷한 수의 노드를 갖게 한다.
● Splay 트리
- Splay 연산 : 최근에 접근한 노드 x를 루트노드에 두어 트리를 재구성하는 연산이다.
- Splay 트리 : 가장 최근에 사용한 노드 x가 트리의 투르노드가 될 때까지 Splay 연산을 반복하여 만들어진 이진트리
● Splay 연산?
- 노드 x : 최근 접근한 노드
- 노드 p : x의 부모 노드
- 노드 g : x의 부모의 부모 노드

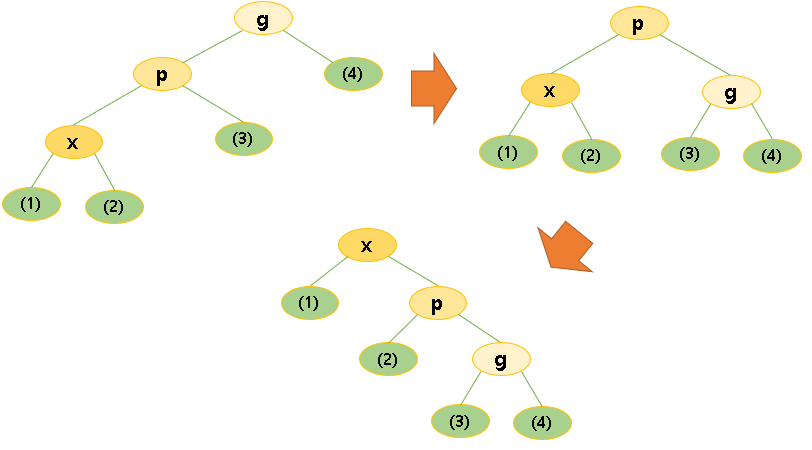
- Zig 회전 (단일 회전) :
p가 루트노드면, p와 x 사이의 간선 연결된 부분(edge joining)을 회전시킨다. - Zig - Zig 회전 (두 개의 단일 회전):
p가 루트노드가 아니고 x와 p가 동일하게 왼쪽 자식들이거나 오른쪽 자식들이면 p와 조부모 g와의 간선 연결(edge joining)을 회전시키고 x와 p의 간선 연결을 회전시킨다. - Zig-Zag :
p가 루트노드도 아니고, x가 왼쪽 자식, p가 오른쪽자식(x 오른쪽자식, p가 왼쪽자식) 이면 x와 p의 간선 연결을 회전시키고 다음에 x와 x의 새로운 부모 p와의 간선 연결을 회전시킨다.
▶Zig 회전
< p가 루트노드일 때 >
x에 다시 접근할 확률이 높기 때문에 (최근 접근했었으므로) 접근에 용이하도록 루트노드에 x를 위치시키고 edge joining을 회전시켜서 트리 구조를 안정화시킨다.

▶Zig-Zig 회전
< p가 루트노드가 아닐 때 >
< x와 p가 동일하게 왼족 자식들 또는 오른쪽 자식들을 가질 때 >
▣ AVL 트리
AVL 트리는 왼쪽 서브트리와 오른쪽 서브트리의 높이를 중점적으로, 또는 노드의 개수를 중점적으로 균형을 잡은 BS 트리의 변형 트리다.
● 변형 BS 트리인 AVL 트리 탄생 배경과 개념
- 노드의 삽입과 삭제 시, 노드의 key 값과 서브트리의 key 값 사이의 관계를 유지하며 균형을 유지하는 건 쉽지가 않다.
- 아무리 좌우 균형을 맞추려해도 완벽히 맞기 어려울 수 있으므로 완벽한 균형은 아니여도 좀 더 균형 잡힌 트리를 만들어보자고 제시함.
- 무너진 균형의 정도는 작아야 하며 평균 탐색 길이도 완전 균형 트리의 탐색 길이와 큰 차이가 없어야 한다.
- 거의 완전한 규형 트리의 형태로 높이가 균형 잡힌 높이 균형 트리다.
- 직접 탐색 성능이 매우 좋다.
● AVL 트리 조건
- 특정 노드의 왼쪽 서브트리 높이와 오른쪽 서브트리 높이가 최대 1만큼 차이난다. (0이 아니어도 된다)
- 삽입, 삭제로 높이 차이가 1정도 나는 건 허용한다.
▣ BB 트리
BB 트리는 Bound-Balanced 트리란 의미로, 거의 완전하게 무게가 균형잡힌 트리다.
● BB 트리?
- 각 노드의 왼쪽 & 오른쪽 서브트리 무게가 균형을 유지하는 트리다.
- √2-1 < 왼쪽_서브트리_무게 / 오른쪽_서브트리_무게 < √2+1
수식으로 설명을 하자면,
- β 를 균형을 제어하기 위한 인수라 할 때, 균형 β ( 0 < <= 1/2 )는 임의의 노드 x에 대해 x의 한 쪽 서브트리에 x의 자식 노드 수의 비율이 β 와 1-β 사이에 있도록 제한하는 경우다.
- 즉, β = 1/2 라면, 왼쪽 서브트리와 오른쪽 서브트리가 같은 수의 노드를 가져야 한다.
- β = 1/4 라면, 한 쪽 서브트리는 다른 쪽 서브트리에 비해 3배의 노드 수를 가지는 것이 허용된다는 말이다.
- β = 1/2에 가까울수록, balance가 엄격하게 유지되는 트리의 형태라 할 수 있다.
즉 정리하면,
Splay 트리는 최근 탐색된 노드를 루트노드로 올려서 탐색 비용을 줄이는 BS 트리 구조고,
AVL 트리는 트리의 왼쪽, 오른쪽 서브트리 높이를 조절하여 트리의 균형을 유지하는 BS 트리 구조고,
BB 트리는 트리의 왼쪽, 오른쪽 서브트리 노드 개수 (무게) 를 조절하여 트리의 균형을 유지하는 BS 트리 구조다.
결국에 AVL 트리와 BB 트리 모두 균형트리라고 말하며, 각각 무게나 높이에 제한 조건을 두어 균형을 유지하게끔 동작한다. 이 때 균형을 유지하도록 하기 위해 드는 비용(O(log_2 n)개의 노드 옮겨야함)은 완벽하게 트리의 좌우가 균형잡힐 때보단 훨씬 적은 비용(O(n)개의 노드 옮겨야함)을 요구한다.
'Programming > Data Structure' 카테고리의 다른 글
| [개념] 선택트리 selection tree - 승자트리 winner tree, 패자트리 loser tree (2) | 2020.09.23 |
|---|---|
| [C++] 힙 코드 구현 방법 heap (0) | 2020.09.22 |
| [C++] 이진트리 코드 구현 방법 binary tree (0) | 2020.09.21 |
| [C++] 원형 연결 리스트 코드 구현 방법 Circular linked list (1) | 2020.09.11 |
| [C++] 이중연결리스트 코드 구현 방법 Doubly linked list (0) | 2020.09.10 |



