배치 정규화 2015년에 제안된 방법이지만, 많은 연구자와 기술자들이 사용하고 그 효과가 입증된 방법입니다.
배치 정규화를 이용하는 이유들은 다음과 같습니다.
- 학습을 빨리 진행할 수 있다. (학습 속도 개선)
- 초깃값에 크게 의존하지 않는다. (골치 아픈 초깃값 선택 장애를 겪지 않아도 됨)
- 오버피팅을 억제한다. (드롭아웃 등의 필요성 감소)
# 배치 정규화란?
그럼 배치 정규화의 기본 아이디어를 알아봅시다.
배치 정규화는 각 층에서의 활성화값이 적당히 분포되도록 조정하는 것을 목표로 합니다.
그래서 데이터 분포를 정규화하는 '배치 정규화 Batch Norm 계층'을 신경망에 삽입해서 이용합니다.

학습 시 미니배치를 단위로 정규화하는 방식을 사용합니다.
데이터 분포가 평균이 0, 분산이 1이 되도록 정규화하고 수식으로 나타내면 다음과 같습니다.




미니배치 B 라는 m 개의 입력 데이터의 집합에 대해
평균 (μ)과 분산 (σ^2)을 구하고,
입력 데이터를 평균이 0, 분산이 1이 되게 정규화합니다.
ε 을 10e-7과 같이 작은 값으로 두어, 0으로 나누는 일이 없도록 합니다.
위에서 마지막 식은 단순히 입력 데이터 x_i를 X̂ 로 변환하는 일을 합니다.
이 처리를 활성화 함수의 앞(혹은 뒤)에 삽입해서 데이터 분포가 덜 치우치게 할 수 있습니다.
또, 배치 정규화 계층마다 이 정규화된 데이터에 고유한 확대 scale와 이동 shift 변환을 수행합니다. 수식은 아래와 같습니다.

γ 는 확대를, β 는 이동을 담당합니다.
두 값은 처음에는 γ = 1, β = 0부터 시작하고, 학습하면서 적합한 값으로 조정합니다.
γ = 1은 1배 확대, β = 0은 이동하지 않음을 의미합니다. 즉, 원본 그대로 시작한다는 의미입니다.
여기까지가 배치 정규화의 알고리즘이고, 이 알고리즘이 신경망에서 순전파 때 적용됩니다. 이를 그래프로 표현하면 다음과 같습니다.

# 배치 정규화의 효과
배치 정규화 계층을 사용한 실험을 해보겠습니다.
MNIST 데이터셋을 사용하여 배치 정규화 계층을 사용할 때와 사용하지 않을 때의 학습 진도 변화를 비교해보겠습니다.
파이썬으로 배치 정규화 계층을 구현한 코드입니다.
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.optimizer import SGD, Adam
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 학습 데이터를 줄임
x_train = x_train[:1000]
t_train = t_train[:1000]
max_epochs = 20
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
def __train(weight_init_std):
bn_network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
weight_init_std=weight_init_std, use_batchnorm=True)
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
weight_init_std=weight_init_std)
optimizer = SGD(lr=learning_rate)
train_acc_list = []
bn_train_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for _network in (bn_network, network):
grads = _network.gradient(x_batch, t_batch)
optimizer.update(_network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
bn_train_acc = bn_network.accuracy(x_train, t_train)
train_acc_list.append(train_acc)
bn_train_acc_list.append(bn_train_acc)
print("epoch:" + str(epoch_cnt) + " | " + str(train_acc) + " - " + str(bn_train_acc))
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
return train_acc_list, bn_train_acc_list
# 그래프 그리기==========
weight_scale_list = np.logspace(0, -4, num=16)
x = np.arange(max_epochs)
for i, w in enumerate(weight_scale_list):
print( "============== " + str(i+1) + "/16" + " ==============")
train_acc_list, bn_train_acc_list = __train(w)
plt.subplot(4,4,i+1)
plt.title("W:" + str(w))
if i == 15:
plt.plot(x, bn_train_acc_list, label='Batch Normalization', markevery=2)
plt.plot(x, train_acc_list, linestyle = "--", label='Normal(without BatchNorm)', markevery=2)
else:
plt.plot(x, bn_train_acc_list, markevery=2)
plt.plot(x, train_acc_list, linestyle="--", markevery=2)
plt.ylim(0, 1.0)
if i % 4:
plt.yticks([])
else:
plt.ylabel("accuracy")
if i < 12:
plt.xticks([])
else:
plt.xlabel("epochs")
plt.legend(loc='lower right')
plt.show()
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
from collections import OrderedDict
from common.layers import *
from common.gradient import numerical_gradient
class MultiLayerNetExtend:
"""완전 연결 다층 신경망(확장판)
가중치 감소, 드롭아웃, 배치 정규화 구현
Parameters
----------
input_size : 입력 크기(MNIST의 경우엔 784)
hidden_size_list : 각 은닉층의 뉴런 수를 담은 리스트(e.g. [100, 100, 100])
output_size : 출력 크기(MNIST의 경우엔 10)
activation : 활성화 함수 - 'relu' 혹은 'sigmoid'
weight_init_std : 가중치의 표준편차 지정(e.g. 0.01)
'relu'나 'he'로 지정하면 'He 초깃값'으로 설정
'sigmoid'나 'xavier'로 지정하면 'Xavier 초깃값'으로 설정
weight_decay_lambda : 가중치 감소(L2 법칙)의 세기
use_dropout : 드롭아웃 사용 여부
dropout_ration : 드롭아웃 비율
use_batchNorm : 배치 정규화 사용 여부
"""
def __init__(self, input_size, hidden_size_list, output_size,
activation='relu', weight_init_std='relu', weight_decay_lambda=0,
use_dropout = False, dropout_ration = 0.5, use_batchnorm=False):
self.input_size = input_size
self.output_size = output_size
self.hidden_size_list = hidden_size_list
self.hidden_layer_num = len(hidden_size_list)
self.use_dropout = use_dropout
self.weight_decay_lambda = weight_decay_lambda
self.use_batchnorm = use_batchnorm
self.params = {}
# 가중치 초기화
self.__init_weight(weight_init_std)
# 계층 생성
activation_layer = {'sigmoid': Sigmoid, 'relu': Relu}
self.layers = OrderedDict()
for idx in range(1, self.hidden_layer_num+1):
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
if self.use_batchnorm:
self.params['gamma' + str(idx)] = np.ones(hidden_size_list[idx-1])
self.params['beta' + str(idx)] = np.zeros(hidden_size_list[idx-1])
self.layers['BatchNorm' + str(idx)] = BatchNormalization(self.params['gamma' + str(idx)], self.params['beta' + str(idx)])
self.layers['Activation_function' + str(idx)] = activation_layer[activation]()
if self.use_dropout:
self.layers['Dropout' + str(idx)] = Dropout(dropout_ration)
idx = self.hidden_layer_num + 1
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])
self.last_layer = SoftmaxWithLoss()
def __init_weight(self, weight_init_std):
"""가중치 초기화
Parameters
----------
weight_init_std : 가중치의 표준편차 지정(e.g. 0.01)
'relu'나 'he'로 지정하면 'He 초깃값'으로 설정
'sigmoid'나 'xavier'로 지정하면 'Xavier 초깃값'으로 설정
"""
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
for idx in range(1, len(all_size_list)):
scale = weight_init_std
if str(weight_init_std).lower() in ('relu', 'he'):
scale = np.sqrt(2.0 / all_size_list[idx - 1]) # ReLUを使う場合に推奨される初期値
elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
scale = np.sqrt(1.0 / all_size_list[idx - 1]) # sigmoidを使う場合に推奨される初期値
self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
self.params['b' + str(idx)] = np.zeros(all_size_list[idx])
def predict(self, x, train_flg=False):
for key, layer in self.layers.items():
if "Dropout" in key or "BatchNorm" in key:
x = layer.forward(x, train_flg)
else:
x = layer.forward(x)
return x
def loss(self, x, t, train_flg=False):
"""손실 함수를 구한다.
Parameters
----------
x : 입력 데이터
t : 정답 레이블
"""
y = self.predict(x, train_flg)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W**2)
return self.last_layer.forward(y, t) + weight_decay
def accuracy(self, X, T):
Y = self.predict(X, train_flg=False)
Y = np.argmax(Y, axis=1)
if T.ndim != 1 : T = np.argmax(T, axis=1)
accuracy = np.sum(Y == T) / float(X.shape[0])
return accuracy
def numerical_gradient(self, X, T):
"""기울기를 구한다(수치 미분).
Parameters
----------
x : 입력 데이터
t : 정답 레이블
Returns
-------
각 층의 기울기를 담은 사전(dictionary) 변수
grads['W1']、grads['W2']、... 각 층의 가중치
grads['b1']、grads['b2']、... 각 층의 편향
"""
loss_W = lambda W: self.loss(X, T, train_flg=True)
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)])
if self.use_batchnorm and idx != self.hidden_layer_num+1:
grads['gamma' + str(idx)] = numerical_gradient(loss_W, self.params['gamma' + str(idx)])
grads['beta' + str(idx)] = numerical_gradient(loss_W, self.params['beta' + str(idx)])
return grads
def gradient(self, x, t):
# forward
self.loss(x, t, train_flg=True)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 결과 저장
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.params['W' + str(idx)]
grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
if self.use_batchnorm and idx != self.hidden_layer_num+1:
grads['gamma' + str(idx)] = self.layers['BatchNorm' + str(idx)].dgamma
grads['beta' + str(idx)] = self.layers['BatchNorm' + str(idx)].dbeta
return grads
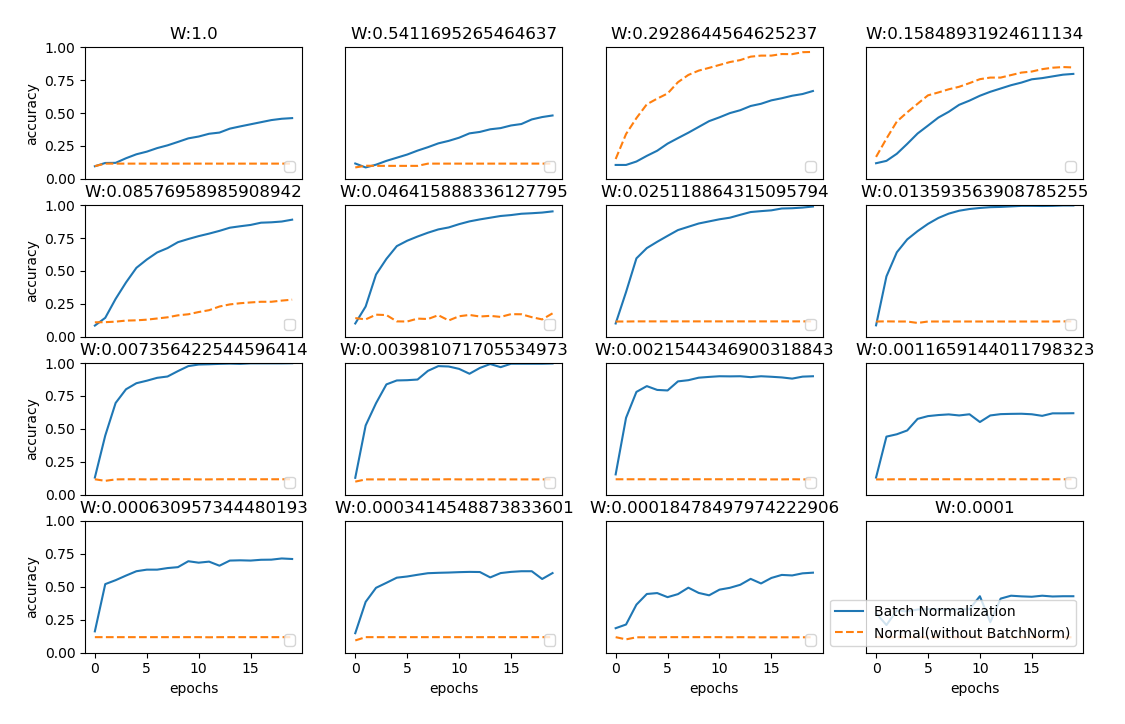
거의 모든 경우에서 배치 정규화를 사용할 때 학습 진도가 빠른 것을 볼 수 있습니다. 배치 정규화를 이용하지 않으면 초깃값이 잘 분포되어 있지 않는 경우엔 아예 학습이 진행되지 않는 것도 볼 수 있습니다.
정리하면, 배치 정규화를 사용하면 가중치 초깃값에 크게 의존하지 않아도 되고, 학습이 빨라집니다.
소스 코드는 Deep learning from scratch의 github 에서 자세히 확인하실 수 있습니다.
https://github.com/oreilly-japan/deep-learning-from-scratch-2
[출처] Deep Learning from Scratch, ゼロ から作る
'Computer Science > Deep Learning' 카테고리의 다른 글
| [비전공자용] [Python] 하이퍼파라미터 최적화 Hyperparameter Optimization (0) | 2020.07.10 |
|---|---|
| [비전공자용] 오버피팅 Overfitting 억제법 - 1.가중치 감소 2.드롭아웃 Dropout (0) | 2020.07.10 |
| [비전공자용] [Python] Xavier Initialization (Xavier 초기화) & He Initialization (He 초기화) (0) | 2020.07.10 |
| [비전공자용] [Python] 모멘텀, AdaGrad, Adam 최적화기법 (0) | 2020.07.09 |
| [비전공자용] 확률적 경사 하강법 SGD 의 단점 (0) | 2020.07.08 |



