신경망 학습에서 가중치 초깃값을 어떻게 정하느냐에 따라 신경망 학습이 성공할 수도 있고 실패할 수도 있습니다.
은닉층 Hidden Layer의 활성화값(활성화 함수의 출력 데이터, 계층 사이를 흐르는 데이터)의 분포를 잘 관찰하면 가중치를 어떻게 설정해야 좋을지 알 수 있습니다.
은닉층이 5개이고, 각 층의 뉴런이 100개씩 존재한다고 합시다. 입력 데이터로서 1,000개의 데이터를 표준정규분포로 랜덤하게 생성하여 5층 신경망에 흘리고 각 층의 활성화값을 비교해 볼 것 입니다.
활성화 함수로는 시그모이드 Sigmoid 함수를 사용하고, 각 층의 활성화 결과를 activations 변수에 저장합니다.
가중치 초깃값을 표준정규분포로 설정하고 표준편차를 변화시키면서 활성화 결과를 히스토그램으로 보겠습니다.
파이썬 코드로 구현하면 아래와 같습니다.
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def ReLU(x):
return np.maximum(0, x)
def tanh(x):
return np.tanh(x)
input_data = np.random.randn(1000, 100) # 1000개의 데이터, 표준정규분포로 1000행 100열 행렬생성
node_num = 100 # 각 은닉층의 노드(뉴런) 수
hidden_layer_size = 5 # 은닉층이 5개
activations = {} # 이곳에 활성화 결과를 저장
x = input_data
for i in range(hidden_layer_size):
if i != 0:
x = activations[i-1]
# 초깃값을 다양하게 바꿔가며 실험해보자!
w = np.random.randn(node_num, node_num) * 1 # 1. 표준편차 1
# w = np.random.randn(node_num, node_num) * 0.01 # 2. 표준편차 0.01
# w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num) # 3. Xavier,표준편차 1/√n
# w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num) # 4. He,표준편차 √(2/n)
a = np.dot(x, w)
# 활성화 함수도 바꿔가며 실험해보자!
z = sigmoid(a)
# z = ReLU(a)
# z = tanh(a)
activations[i] = z
# 히스토그램 그리기
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + "-layer")
if i != 0: plt.yticks([], [])
plt.xlim(0.0, 1.0)
# plt.ylim(0, 7000)
plt.hist(a.flatten(), 30, range=(0,1))
plt.show()
# 활성화 함수 Sigmoid 함수
1. 가중치 초깃값 정규분포 표준편차 = 1

각 층의 활성화값이 0과 1에 치우쳐 분포되어 있습니다. 데이터가 0과 1에 치우쳐 분포하면 역전파의 기울기 값이 점점 작아지다가 사라져서 기울기 손실 Gradient vanishing 문제가 발생합니다. 층이 더 깊은 신경망에서는 더 심각한 결과를 초래합니다.
2. 가중치 초깃값 정규분포 표준편차 = 0.01

이번엔 0.5 근처에 활성화값이 집중되어 있습니다. 기울기 소실 문제는 일어나지 않겠지만, 활성화값들이 치우쳤다는 것은 다수의 뉴런이 거의 같은 값을 출력하고 있어서 뉴런을 여러 개 둔 의미가 없다는 의미여서 큰 문제가 됩니다. 즉, 뉴런 1개나 뉴런 100개나 거의 같은 값을 출력한다면 표현력이 제한되었다고 볼 수 있습니다.
각 층의 활성화값은 적당히 고루 분포되어야 합니다. 층과 층 사이에 적당히 다양한 데이터가 흐르게 해야 신경망 학습이 효율적으로 이뤄지기 때문입니다. 반대로 치우친 데이터가 흐르면 기울기 소실이나 표현력 제한 문제에 빠져 학습이 잘 이뤄지지 않는 경우가 생깁니다.
3. 가중치 초깃값으로 Xavier 초깃값 이용
일반적인 딥러닝 프레임워크에서 표준적으로 이용하고 있는 Xavier 초깃값을 가중치 초깃값으로 설정한 결과를 보려고 합니다. 각 층의 활성화값들을 광범위하게 분포시키기 위해 가중치의 적절한 분포를 찾고자,
앞 계층의 노드가 n 개일 때 가중치 초깃값을 표준편차가 1/√n 인 정규분포를 갖도록 설정하는 것이 Xavier 초깃값 (Xavier Initialization) 입니다.


Xavier 초깃값을 사용하면 앞 층에 노드가 많을수록 가중치가 좁게 퍼집니다. Xavier 초깃값을 이용해서 코드를 실행하면 아래와 같은 결과를 얻습니다.

결과를 보면, 앞에 두 경우보다 확실히 넓게 분포됨을 알 수 있습니다. 이 경우, 각 층에 흐르는 데이터의 분포가 넓어서 시그모이드 함수의 표현력도 제한받지 않고 학습이 효율적으로 이뤄질 수 있을 것입니다.
오른쪽으로 갈수록 약간씩 분포가 일그러지는데 이는 sigmoid함수 대신에 tanh함수를 이용하면 개선됩니다.
Xavier 초깃값은 활성화 함수가 선형인 것을 전제로 이끌어낸 경우입니다. Sigmoid 함수와 tanh 함수가 좌우 대칭이라 중앙 부근이 선형인 함수라고 볼 수 있습니다. 그래서 Xavier 초깃값을 이용하기에 적당합니다.
반면에 활성화함수로 ReLU를 사용할 경우에는 Xavier 초깃값을 사용하는 것이 적절하지 않습니다. 이 경우에는 가중치 초깃값을 He 초깃값을 사용합니다.
# 활성화 함수 ReLU 함수
He 초깃값은 활성화함수로 ReLU를 사용할 때 특화된 가중치 초기값입니다. 앞 계층의 노드가 n개일 때, 표준편차가 √(2/n) 인 정규분포를 사용합니다. ReLU는 음의 영역이 0이라 더 넓게 분포시키기 위해 Xavier 에 비해 2배의 계수가 필요하다고 직감적으로 해석할 수 있습니다. 그러면 먼저 활성화 함수가 ReLU인 경우 He 초기화를 통해 가중치를 초기화하는 경우부터 결과가 어떻게 되는지 살펴보겠습니다.
1. 가중치 초깃값으로 He 초깃값 이용

ReLU 함수의 특성상 0에서 큰 분포를 가진 것 외에, 모든 층에서 균일하게 분포된 것을 확인 할 수 있습니다.
층이 깊어져도 분포가 균일하게 유지되어 역전파 때도 적절한 값이 나올 것으로 기대할 수 있습니다.
2. 가중치 초깃값으로 Xavier 초깃값 이용

Xavier 초깃값 결과를 보면 층이 깊어지면서 활성화 결과 분포의 치우침이 조금씩 커집니다. 실제로 ReLU를 쓰는 경우에 Xavier 초기화를 이용하면 층이 깊어지면서 활성화값들의 치우침이 커지고 학습할 때 기울기 소실 문제를 일으킵니다.
3. 가중치 초깃값 정규분포 표준편차 = 0.01

각 층의 활성화값들이 아주 작은 값이고 신경망에 아주 작은 데이터가 흐른다는 건 역전파 때 가중치의 기울기 역시 작아진다는 뜻입니다. 이런 경우에는 실제로 학습이 거의 이뤄지지 않습니다.
# MNIST 데이터셋으로 가중치 초깃값 비교
실제 데이터를 가지고 지금까지 배운 가중치 초깃값이 주는 영향을 비교해보려고 합니다.
파이썬 코드는 아래와 같습니다.
# coding: utf-8
import os
import sys
sys.path.append(os.pardir) # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD
# 0. MNIST 데이터 읽기==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 1. 실험용 설정==========
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)
networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():
networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10, weight_init_std=weight_type)
train_loss[key] = []
# 2. 훈련 시작==========
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in weight_init_types.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizer.update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print("===========" + "iteration:" + str(i) + "===========")
for key in weight_init_types.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 3. 그래프 그리기==========
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()
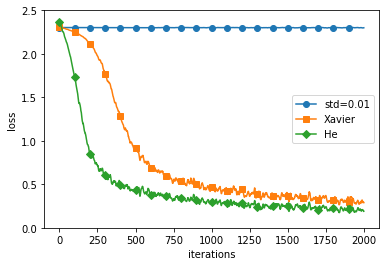
결과를 확인해보면 표준편차가 0.01인 정규분포인 경우에는 학습이 전혀 이뤄지지 않는 것을 확인할 수 있습니다. 가중치가 0으로 수렴하면서 역전파를 할 때 기울기가 너무 작아져 가중치가 거의 갱신되지 않아서 이런 결과를 나타낸 것입니다. 이 예제의 경우에는 He 초깃값 쪽이 학습 진도가 더 빠른 것을 확인할 수 있습니다.
위 결과를 종합해보면,
활성화 함수로 ReLU를 사용할 때는 He 초깃값을,
sigmoid나 tanh 등의 S자 모양 곡선을 사용할 때는 Xavier 초깃값을
사용하는 게 좋습니다.
[출처] Deep Learning from Scratch, ゼロ から作る
'Computer Science > Deep Learning' 카테고리의 다른 글
| [비전공자용] 오버피팅 Overfitting 억제법 - 1.가중치 감소 2.드롭아웃 Dropout (0) | 2020.07.10 |
|---|---|
| [비전공자용] [Python] 배치 정규화 Batch Normalization (2) | 2020.07.10 |
| [비전공자용] [Python] 모멘텀, AdaGrad, Adam 최적화기법 (0) | 2020.07.09 |
| [비전공자용] 확률적 경사 하강법 SGD 의 단점 (0) | 2020.07.08 |
| [비전공자용] [Python] 오차역전파법 Backpropagation 신경망 구현 (0) | 2020.07.08 |



